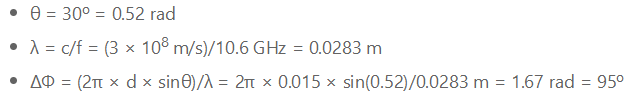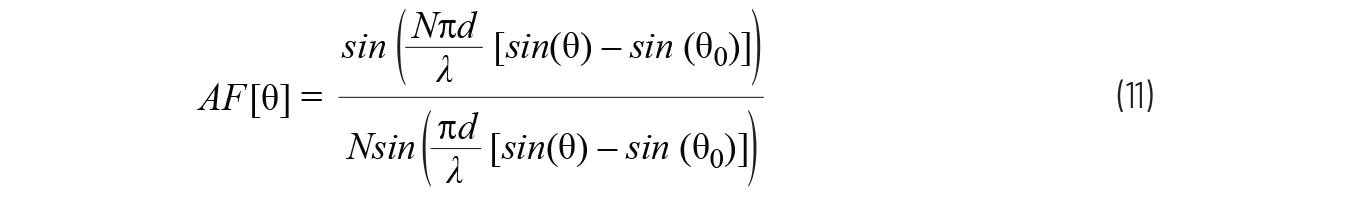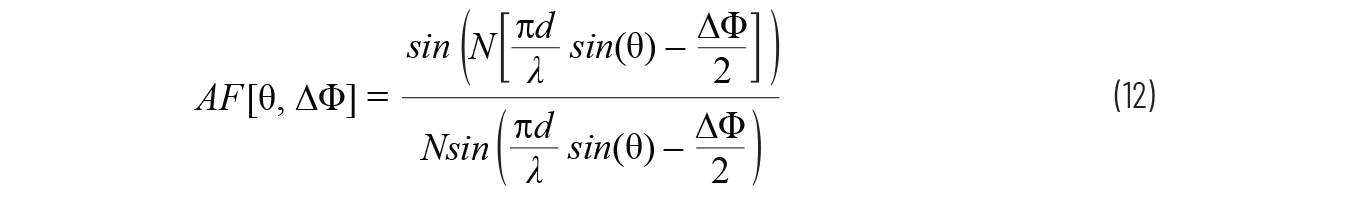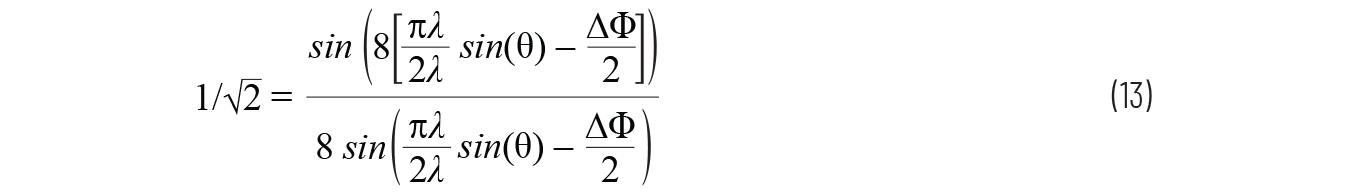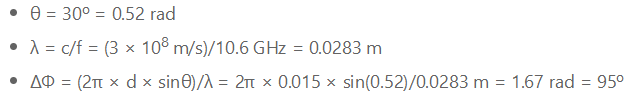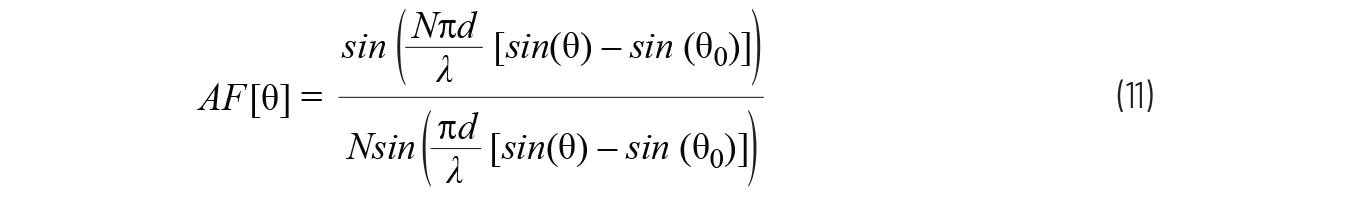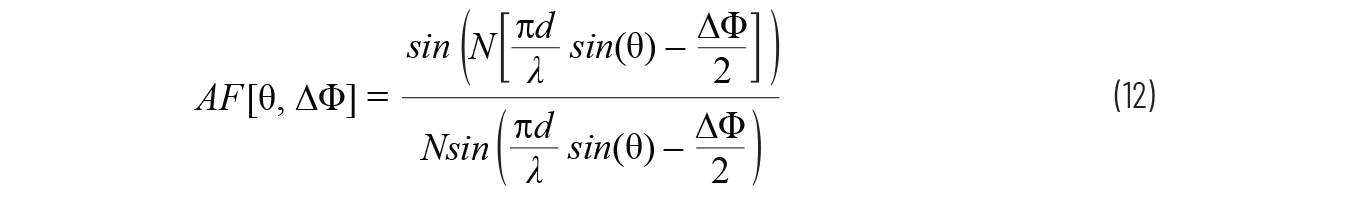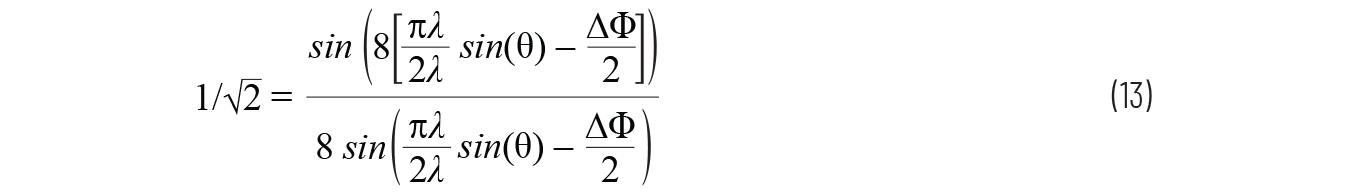本系列文章的目的并非培養(yǎng)天線設(shè)計工程師，而是向使用相控陣子系統(tǒng)或器件的工程師展現(xiàn)他們的工作對相控陣天線方向圖的影響。

 

波束方向

 

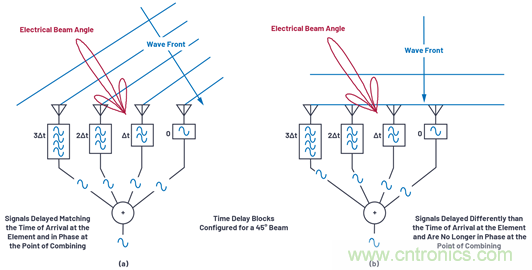
首先，讓我們來看看一個直觀的相控陣波束轉(zhuǎn)向示例。圖1是一個簡單的圖示，描繪了波前從兩個不同方向射向四個天線元件。在接收路徑上的每個天線元件后面都會產(chǎn)生延時，之后所有四個信號再匯總到一起。在圖1a中，該延時與波前到達每個元件的時間差一致。在本例中，產(chǎn)生的延時會導致四個信號同相到達合并點。這種一致的合并會增強組合器輸出的信號。在圖1b中，產(chǎn)生的延時相同，但在本例中，波前與天線元件垂直?，F(xiàn)在產(chǎn)生的延時與四個信號的相位不一致，因此組合器輸出會被大幅削弱。

 

圖1.理解轉(zhuǎn)向角度。

 

在相控陣中，延時是波束轉(zhuǎn)向所需的可量化變量。但也可以通過相移來仿真延時，這在許多實現(xiàn)中是十分常見且實用的做法。我們將在介紹波束斜視的部分討論延時與相移的影響，但目前我們先來了解相移實現(xiàn)，然后推導相應(yīng)相移的波束轉(zhuǎn)向計算。

 

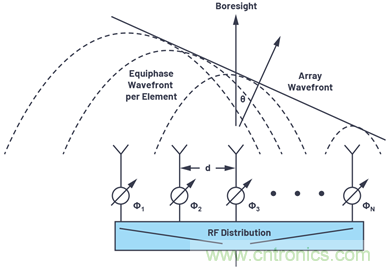
圖2所示為使用移相器而非延時的相控陣排列。請注意，我們將瞄準線方向(θ = 0°)定義為垂直于天線正面。瞄準線右側(cè)定義為正角θ，瞄準線左側(cè)定義為負角。

 

圖2.使用RF移相器的相控陣概念。

 

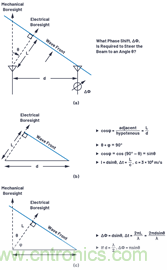
要顯示波束轉(zhuǎn)向所需的相移，可以在相鄰元件之間繪制一組直角三角形，如圖3所示。其中，ΔΦ表示這些相鄰元件之間的相移。

 

圖3.相移ΔΦ與波束轉(zhuǎn)向角度的推導。

 

圖3a定義了這些元件之間的三角恒等式，各元件之間相隔距離用(d)表示。波束指向與瞄準線相距θ的方向，波束距離視平線的角度為φ。在圖3b中，我們看到θ與φ的和為90°。這樣我們就可以計算L，因為L = dsin(θ)，L表示波傳播的變量距離。波束轉(zhuǎn)向所需的延時等于波前遍歷該距離L所用的時間。如果將L視作波長的分數(shù)，則相位延遲可以用該延時替代。ΔΦ等式可以定義為相對于θ，如圖3c所示以及等式1中的重復計算。

 

 

如果元件間隔正好等于信號波長的一半，則可以進一步簡化為：

 

 

我們以具體示例來計算這些等式。假設(shè)兩個天線元件間隔15 mm。如果一個10.6 GHz的波前以距離機械瞄準線30°的角度到達，那么這兩個元件之間的最佳相移是多少？

 

 

所以，如果波前以θ = 30°到達，并將相鄰元件的相位移動95°，則可以使兩個元件各自的信號實現(xiàn)一致疊加。這樣就可以使該方向的天線增益達到最大值。

 

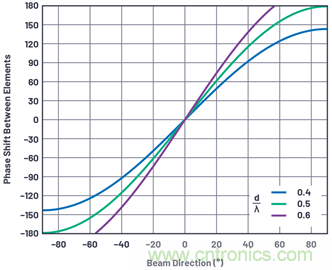
為深入理解相移如何隨著波束方向(θ)而變，圖4以圖形方式繪制了不同條件下的這些等式圖解。從這些圖形中可以觀察到一些有趣的現(xiàn)象。比如，d = λ/2時，瞄準線附近的斜率約為3:1，即等式2中的乘數(shù)π。這種情況還展示出，元件之間達到180°完整相移會使波束方向達到理論相移90°。實際上，在真實的元件方向圖中，這是不可能實現(xiàn)的，但等式的確顯示出理論上的理想值。需要注意的是，d > λ/2時，不存在能夠提供完整波束位移的相移。在后面的文章中，我們將會介紹該情況會導致天線方向圖中的柵瓣，該圖形是第一次表明，d > λ/2情況下的行為有所不同。

 

圖4.三種d/λ情況下，元件之間的相移ΔΦ與波束方向(θ)之間的關(guān)系。
 

等間隔線性陣列

 

上文推導的等式僅適用于兩個元件。但實際的相控陣可能在兩個維度上包含數(shù)千個間隔開的元件。但出于本文用途，我們僅考慮一個維度：線性陣列。

 

線性陣列為單元件寬度，其中包含N個元件。不同線性陣列，間隔可能各有不同，但同一線性陣列通常是等間隔。因此，在本文中，我們將各個元件之間的間隔設(shè)為統(tǒng)一距離d（圖5）。該等間隔線性陣列模型雖然是簡化版，但基本介紹了天線方向圖如何形成以及各種不同的條件。我們可以進一步運用線性陣列原理來理解二維陣列。

 

圖5.等間隔線性陣列(N = 4)。
 

近場與遠場

 

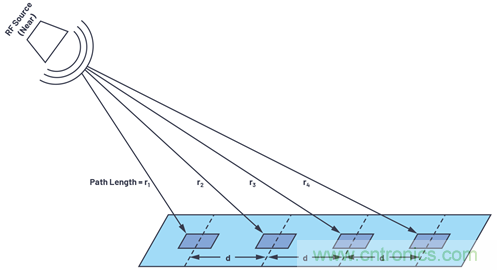
如何將上文針對N = 2的線性陣列推導的公式運用到N = 10,000的線性陣列呢？現(xiàn)在，似乎每個天線元件都以稍微不同的角度指向球形波前，如圖6所示。

 

圖6.RF信號源與線性陣列較近。

 

如果RF源較近，則每個元件的入射角不同。這種情況稱為近場。我們可以算出所有這些角度，有時需要這么做是為了進行天線測試和校準，因為我們的測試裝置只能這么大。但如果RF源較遠，則就是圖7所示的情況。

 

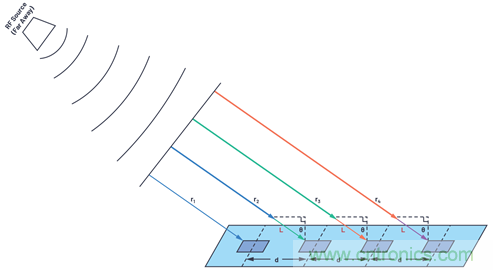
圖7.RF信號源與線性陣列相隔較遠。

 

如果RF源較遠，則球形波前的大半徑會導致大致平行的波傳播路徑。因此，所有波束角均相等，每個相鄰元件的路徑長度(L = d × sinθ)均超過隔壁元件。這樣簡化了數(shù)學計算，意味著我們推導出來的雙元件等式可以應(yīng)用到數(shù)千個元件，但前提是這些元件間隔相同。

 

但在什么情況下可以做出遠場假設(shè)？遠場有多遠？雖然稍顯主觀，但通常而言，遠場定義是超過：

 

 

其中，D表示天線直徑（對于等間隔線性陣列為(N-1) × d）

 

對于小型陣列（D值?。┗虻皖l（λ值大），遠場距離較小。但對于大型陣列（或高頻），遠場距離可能長達數(shù)千米！這樣測試和校準陣列就十分困難。對于這類情況，可以使用更為詳細的近場模型，然后再按比例擴展到真實世界使用的遠場陣列。

 

天線增益、方向性和孔徑

 

在繼續(xù)深入之前，先了解天線增益、方向性和孔徑的定義十分有用。首先介紹增益與方向性，因為這兩個概念經(jīng)常互換使用。天線增益和方向性是相較于各向同性天線而言，各向同性天線是所有方向均勻輻射的理想天線。方向性是指在特定方向上測得的最大功率Pmax與所有方向輻射的平均功率Pav的比值。如果沒有定義方向，則方向性通過等式4確定。/p>

 

 

在比較天線時，方向性是一個有用指標，因為它定義了集中輻射能量的能力。增益與方向性的方向圖相同，但增益包含天線損耗。

 

 

Prad是總輻射功率， Pin是輸入到天線的功率，k表示天線輻射過程中的損耗。

 

接下來，我們將天線方向圖視為三維方向的函數(shù)，將方向性視為波束寬度的函數(shù)。

 

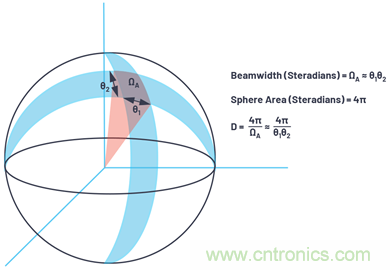
圖8.投射到球體的面積的三維視圖。

 

球體的總表面積是4π2，球體上的面積以球面度為單位定義，等于球體中的4π球面度。因此，來自各向同性輻射體的功率密度為

 

 

采用的單位為(W/m2).

 

球體上的一塊面積有兩個角方向。在雷達系統(tǒng)中，這兩個角方向通常稱作方位角和俯仰角。波束寬度可以描述為每個角方向的函數(shù)（θ1和θ2）：該組合會在球體上形成一塊面積ΩA.

 

ΩA是以球面度為單位表示的波束寬度，可以近似為ΩA ≈ θ1 × θ2.

 

確認ΩA為球體上的面積后，方向性可以表示為

 

 

我們將要考慮的第三個天線術(shù)語是孔徑。天線孔徑表示用于接收電磁波的有效面積，包含相對于波長的函數(shù)。各向同性天線的孔徑為

 

 

增益是相對于各向同性天線而言，產(chǎn)生的有效天線孔徑為

 

 

綜合三個術(shù)語來看，可以將增益視作用于定義輻射方向圖的角的函數(shù)，表示天線中的效率（或損耗）。

 

線性陣列的陣列因子

 

目前，我們能夠預測元件之間的最佳時間（或相位）變量來實現(xiàn)最大天線方向性。但我們非常需要了解和操作完整的天線增益方向圖。這分為兩個主要方面。首先，陣列的每個獨立元件（或許是貼片）都存在增益，稱為元件因子(GE)。其次，通過陣列波束成型會產(chǎn)生增益影響，稱為陣列因子 (GA)。全陣列天線增益方向圖是這兩個因子的組合，如等式10所示。

 

 

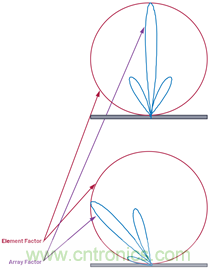
圖9.元件因子和陣列因子。

 

圖9.元件因子和陣列因子。GE表示陣列中單個元件的輻射方向圖。其定義取決于天線的幾何形狀和構(gòu)造，而不是在運行中會發(fā)生變化的因素。知道這一點很重要，因為這會限制總陣列的增益——尤其是靠近視平線時。但由于我們不采用電子控制，因此可以將它保持固定不變，作為總相控陣增益等式的影響因子。在本文中，我們假設(shè)所有獨立元件都有相同的元件因子。

 

接下來重點介紹陣列因子GA。陣列因子的計算基于陣列幾何結(jié)構(gòu)（d表示等間隔線性陣列）和波束權(quán)重（幅度和相位）。推導等間隔線性陣列的陣列因子十分簡單，但本文末尾引用的參考文獻中詳細介紹了相關(guān)內(nèi)容。

 

文獻中使用的等式各有不同，具體取決于線性陣列參數(shù)的定義方式。我們使用本文中的等式，以便與圖2和圖3中的定義保持一致。由于主要問題在于增益如何變化，因此繪制相對于單位增益的標準化陣列因子通常更具指導意義。標準化陣列因子可以寫為等式11。

 

 

 

我們已將波束角度θ0定義為元件之間的相移的函數(shù)θ0；因此，我們也可以將標準化天線因子寫為等式12

 

 

陣列因子等式中假設(shè)的條件包括：

 

●  元件間距相等。

●  元件之間的相移相同。

●  所有元件的幅度相同。

 

接下來，我們利用這些等式繪制多種陣列尺寸的陣列因子。

 

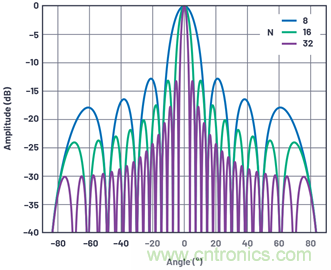
圖10.位于線性陣列瞄準線的標準化陣列因子，其中元件間隔為d = λ/2，元件數(shù)量分別為8、16和32。

 

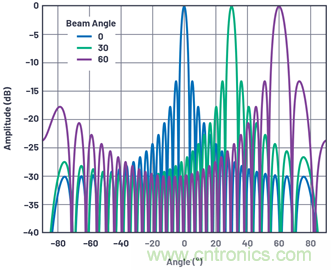
圖11.處于多種波束角度的32元件線性陣列的標準化陣列因子，其中元件間隔為d = λ/2。

 

從這些數(shù)據(jù)中可以觀察到以下幾點：

 

●  第一個旁瓣位于–13 dBc，與元件數(shù)量無關(guān)。這是由陣列因子等式中的sinc函數(shù)決定的。旁瓣可以通過逐漸減少元件中的增益來改善，這一主題將在本系列后續(xù)內(nèi)容中探討。

●  波束寬度隨著元件數(shù)量而減小。

●  掃描的波束離瞄準線越遠，波束寬度會隨之變寬。

●  零點的數(shù)量隨著元件數(shù)量的增加而增多。

 

波束寬度

 

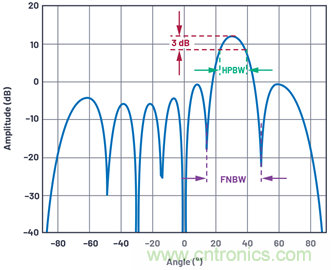
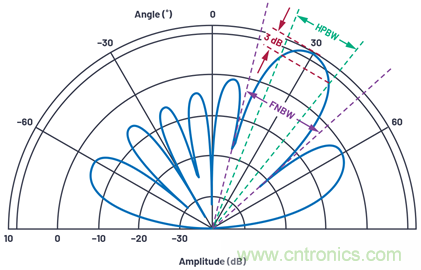
波束寬度是天線角度分辨率的一個指標。最常見的是通過半功率波束寬度(HPBW)或主瓣的零點到零點的間隔(FNBW)定義波束寬度。要找到HPBW，從峰值向下移動3 dB，并測量角距，如圖12所示。

 

圖12.天線波束寬度的定義（所示線性陣列為N = 8，d = λ/2，θ = 30°）。

 

利用我們的標準化陣列因子等式，可以通過將等式3設(shè)為等于半功率級別（3 dB或1/√2）來解算該HPBW。我們假設(shè)機械瞄準線(θ = 0°)、N = 8且d = λ/2。

 

 

然后解算?Φ得出0.35 rad。利用等式1并解算θ：

 

 

該θ是到達3 dB點（即HPBW的一半）的峰值。因此，我們只需要將它乘以2即可獲得3 dB點之間的角距。這會得出12.8°的HPBW。

 

我們可以對等于0的陣列因子重復這個計算，并獲得在前文所述條件下的第一個零點到零點的間隔角度FNBW 28.5°。

 

對于等間隔線性陣列，等式15可計算出HPBW [1,2]的近似值。

 

 

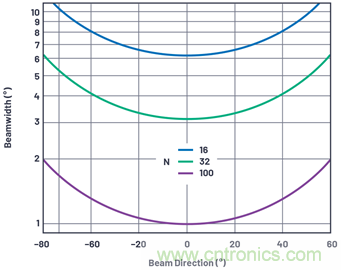
圖13繪制了在λ/2元件間隔條件下多種元件數(shù)量的波束寬度與波束角。

 

圖13.元件數(shù)量為16、32和100時，元件間隔為λ/2的波束寬度與波束角。

 

在此圖中，值得注意的是與業(yè)界正在開發(fā)的陣列尺寸相關(guān)的一些觀察結(jié)果。

 

●  1°波束精度要求存在100個元件。如果方位角和俯仰角都有此要求，則會產(chǎn)生包含10,000個元件的陣列。1°精度只會出現(xiàn)在近乎理想條件下的瞄準線處。在現(xiàn)場陣列中，若要在多種掃描角中保持1°精度，將會進一步增加元件數(shù)量。這一觀察結(jié)果會為超大陣列設(shè)定波束寬度的實際限制。

 

●  1000個元件的陣列是業(yè)界常見陣列。如果每個方向32個元件，則總共擁有1024個元件，靠近瞄準線處會產(chǎn)生小于4°的波束精度。

 

●  256個元件的陣列可以低成本量產(chǎn)，并且仍具有小于10°的波束指向精度。這或許是許多應(yīng)用能夠接受的理想選擇。

 

●  另外還需注意的是，對于上述任何情況，波束寬度在60°偏移處將會翻倍。這是因為分母中有cosθ，受陣列投影縮減的影響；即，從某個角度觀察時，陣列看起來像是縮小的交叉部分。

 

組合元件因子和陣列因子

 

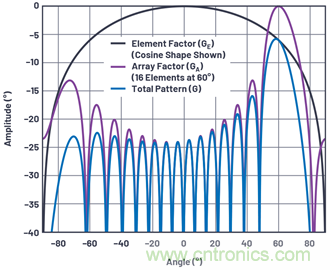
上一節(jié)僅考慮了陣列因子。但為了找出總天線增益，還需要元件因子。圖14描述了一個示例。在該示例中，我們使用一個簡單的余弦形狀作為元件因子，或標準化元件增益GE(θ)。余弦滾降在相控陣分析中十分常見，如果考慮的是平面，則可以將它顯示出來。在寬邊，有一個最大面積。隨著角度遠離寬邊，可見面積會隨著余弦函數(shù)而減小。

 

在上文的λ/2間隔、均勻輻射方向圖、含16個元件的線性陣列中使用了陣列因子GA(θ)。總方向圖是元件因子和陣列因子的線性乘積，因此采用dB刻度，可以將它們相加。

 

圖14.元件因子和陣列因子組合形成總天線方向圖。

 

隨著波束遠離瞄準線的一些觀察結(jié)果：

 

●  主波束的幅值按照元件因子的速率衰減。

●  瞄準線上的旁瓣沒有幅度損失。

●  在原理瞄準線時總體陣列的旁瓣性能下降。

 

天線繪圖：笛卡爾與極坐標

 

目前使用的天線方向圖繪圖一直采用笛卡爾坐標。但采用極坐標繪制天線方向圖也很常見，因為它們更容易表示從天線向外部空間輻射的能量。圖15是圖12的重繪版本，但使用的是極坐標。請注意，采用的數(shù)據(jù)完全相同，只是以極坐標系統(tǒng)重新繪制。能夠以任一表示方法呈現(xiàn)天線方向圖是十分有意義的，因為這兩種系統(tǒng)在文獻中均會使用。在本系列的大部分內(nèi)容中，我們將使用笛卡爾坐標，因為該表示方法更容易比較波束寬度和旁瓣性能。

 

圖15.N = 8，d = λ/2，θ = 30°的極坐標天線方向性繪圖。

 

陣列相互作用

 

截至目前，所有圖解和文字均描述的是陣列接收的信號。那么對于發(fā)射陣列會有何不同呢？幸運的是，大多數(shù)天線性陣列存在相互作用關(guān)系。因此，接收天線的所有圖解、等式和術(shù)語與發(fā)射天線相同。有時將波束視為由陣列接收會更容易理解。而有時，比如就柵瓣而言，或許將陣列視為發(fā)射波束更為直觀。在本文中，我們通常將陣列描述為接收信號。但如果對您而言難以想象，也可以從發(fā)射角度思考相同的概念。

 

小結(jié)

 

本系列第1部分至此結(jié)束。本文介紹了關(guān)于相控陣波束轉(zhuǎn)向的概念。推導并以圖形方式展示了用來計算波束轉(zhuǎn)向的陣列相移的等式。然后通過觀察元件數(shù)量、元件間隔和波束角對天線響應(yīng)的影響，定義了陣列因子和元件因子。最后，展示了以笛卡爾與極坐標表示的天線方向圖對比。

 

在本系列后續(xù)文章中，將進一步探討相控陣天線方向圖和減損。我們將研究天線變窄如何導致旁瓣縮小，柵瓣是如何形成的，以及在寬帶系統(tǒng)中相移與延時的影響。本系列最后將對延遲塊的有限分辨率進行分析，介紹它如何形成量化旁瓣并降低波束分辨率。

 

參考電路

 

Balanis, Constantine A. 天線理論：分析與設(shè)計。第三版，Wiley，2005年。

 

Mailloux, Robert J. 相控陣天線手冊。第二版，Artech House，2005年。

 

O’Donnell, Robert M. “雷達系統(tǒng)工程：簡介。”IEEE，2012年6月。

 

Skolnik, Merrill. 雷達手冊。第三版，McGraw-Hill，2008年。

 

 

推薦閱讀：