【導(dǎo)讀】我們將研究CCM反激式轉(zhuǎn)換器于電壓模式下被漏電感影響的小信號(hào)響應(yīng)�����。我們將從大信號(hào)模型逐步邁向逐漸簡(jiǎn)化的小信號(hào)電路原理圖���,以建立最簡(jiǎn)單的線性版本。從這最終的電路���,我們將提取控制-輸出傳遞函數(shù)����,并顯示漏電感如何影響傳遞函數(shù)分母的品質(zhì)因數(shù)�。
從大信號(hào)到小信號(hào)
當(dāng)您想獲得一個(gè)復(fù)雜電路的傳遞函數(shù)時(shí),您的目標(biāo)是減少?gòu)?fù)雜度�,以便通過(guò)最簡(jiǎn)單的電路原理圖進(jìn)行分析。但是����,當(dāng)您在減少電路的過(guò)程中–通過(guò)因式分解、簡(jiǎn)化表達(dá)式����、忽略變量等–您必須測(cè)試您的新電路,并與最初的電路響應(yīng)進(jìn)行比較��。在最初的響應(yīng)和您隨后的簡(jiǎn)化版本的響應(yīng)之間的任何偏差都表明您弄錯(cuò)了��,或者您作的假設(shè)過(guò)于簡(jiǎn)單化 :丟棄這電路并回到前一步重做���。遵照這步驟����,您肯定進(jìn)展很慢����,但卻很仔細(xì),您可立即發(fā)現(xiàn)和改正錯(cuò)誤���。沒(méi)有什么比在結(jié)束時(shí)發(fā)現(xiàn)錯(cuò)誤而同時(shí)您意識(shí)到在一個(gè)中間步驟就出了問(wèn)題更令人沮喪的了��!
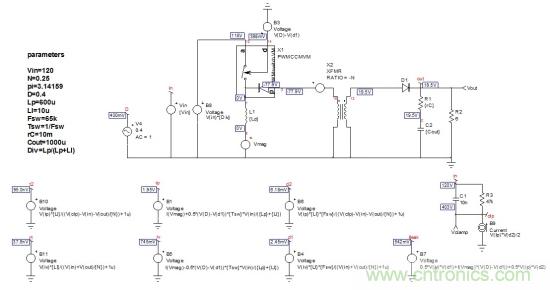
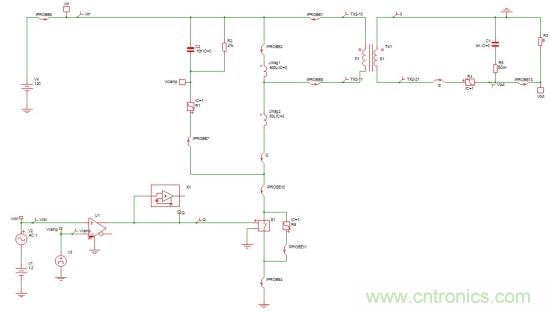
圖1:這開(kāi)環(huán)大信號(hào)電路原理圖是我們的起始電路�����,其動(dòng)態(tài)響應(yīng)將用作后面步驟的參考
首先我們用第二部分介紹的小信號(hào)版本代替大信號(hào)PWM開(kāi)關(guān)模型���。然后����,我們可運(yùn)行一個(gè)交流仿真���,并驗(yàn)證操作點(diǎn)和響應(yīng)是相同的��。非線性模型在圖1中��,而小信號(hào)版本出現(xiàn)在圖2中����。占空比已分為兩個(gè)源��,一個(gè)用于靜態(tài)占空比���,一個(gè)用于交流調(diào)制����。
偏置點(diǎn)與圖1中的相同說(shuō)明第一步是正確的��。我們來(lái)看看這兩個(gè)比較電路的頻率響應(yīng)如何。我們已采集了如圖3 的波特圖:幅值和相位曲線重疊�����,驗(yàn)證了我們的第一步����。
圖2中的電路圖是正確的但相當(dāng)復(fù)雜�。如上所述,小信號(hào)分析意味著盡可能簡(jiǎn)化電路����,并將各種不同元件重新整理成一個(gè)更有意義的架構(gòu)。
圖2:PWM開(kāi)關(guān)由小信號(hào)版本替代���,并對(duì)參考頻率響應(yīng)進(jìn)行了電路動(dòng)態(tài)響應(yīng)檢查
圖3:兩個(gè)電路的波特圖完全重疊�����,驗(yàn)證了第一步�。
我們插入的PWM開(kāi)關(guān)模型確實(shí)是線性版本�����,我們無(wú)需研究它。然而�,計(jì)算峰谷電流、鉗位電壓等的所有源仍然是大信號(hào)運(yùn)算����,我們需要將其線性化。幸運(yùn)的是�����,這有些源在我們的交流分析中是不需要的的如Ip和d2��。
源線性化
您有兩個(gè)選擇��,如果您想線性化這些源�。您可通過(guò)小的勵(lì)磁改變每一變量–您看到的某些變量中的小帽子^ - 并整理交流和直流項(xiàng)以形成兩個(gè)獨(dú)立的等式:一個(gè)靜態(tài)和一個(gè)動(dòng)態(tài)的表達(dá)式。靜態(tài)的表達(dá)式描述了操作點(diǎn)–此處我們并不需要它–而動(dòng)態(tài)的表達(dá)式是我們想要的��。采用這技術(shù)的問(wèn)題是您獲得的項(xiàng)和交叉產(chǎn)品的數(shù)量��,特別是變量超過(guò)兩個(gè)��。整理這些項(xiàng)以形成交流和直流等式���,有時(shí)可能是繁瑣的和錯(cuò)誤的源�。我們?cè)囍捎霉鹊纂娏鞯亩x:
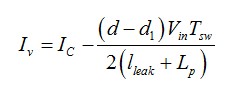
(1)
這里有3個(gè)變量,Ic, d 和d1�����。如果我們少量改變每一變量�,得出
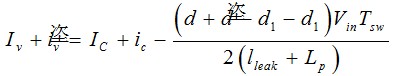
(2)
展開(kāi)為
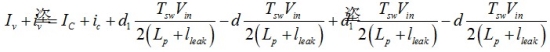
(3)
現(xiàn)在合并交流和直流項(xiàng)�,我們有兩個(gè)定義:
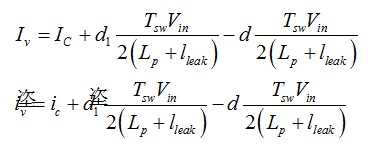
(4)
如果我們定義兩個(gè)系數(shù)kivd 和kivd1為
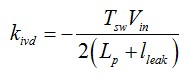
(5)
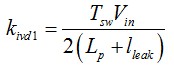
(6)
(4)中的動(dòng)態(tài)等式可重新整理為
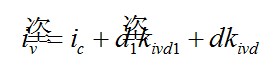
(7)
靜態(tài)系數(shù)kivd 和kivd1將被作為參數(shù)在捕獲的電路圖中傳遞���,并在仿真開(kāi)始前預(yù)估。
另一現(xiàn)有的選擇是不用整理而以更快的方式獲得小信號(hào)系數(shù)如kivd 和kivd1���。分步操作是簡(jiǎn)單的,但表達(dá)式很復(fù)雜���,并有多個(gè)變量��,它很快成為困難的工作�����,您無(wú)法通過(guò)解算器如Mathcad?自動(dòng)求解����。一組不相關(guān)(獨(dú)立) 的變量給出更快的方法����,包括使用偏微分法��,如下所示:
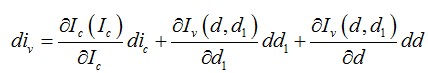
(8)
或使用小信號(hào)記法
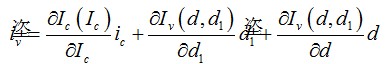
(9)
在這里��,交流項(xiàng)系數(shù)只有從這偏微分法獲得��。將該方法應(yīng)用到圖2中的d1發(fā)生器得出
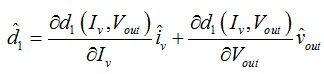
(10)
從中導(dǎo)出
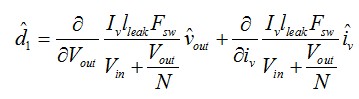
(11)
考慮kd1vo 和kd1iv系數(shù)�,我們可將(11)改寫為
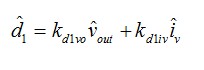
(12)
其中
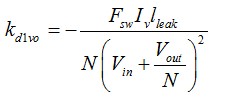
(13)
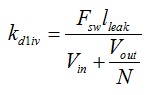
(14)
現(xiàn)在我們有線性的d1 和Iv源����,我們可更新和簡(jiǎn)化電路圖圖2����。結(jié)果如圖4:在參數(shù)文本窗口中計(jì)算表達(dá)式(5)、(6)和(13)���、(14)。現(xiàn)在這圖中的所有源都是小信號(hào)類型����?�?焖俚慕涣鞣治鲲@示,頻率響應(yīng)的幅值和相位完全與圖3匹配����。
簡(jiǎn)化電路原理圖
我們可從這電路原理圖開(kāi)始分析線性轉(zhuǎn)換器�。不過(guò)可能需要進(jìn)一步的簡(jiǎn)化和整理�����。例如,在控制-輸出傳遞函數(shù)中��,輸入電壓是Vin恒定的�,
因此�,連接到輸入電壓的節(jié)點(diǎn)“a”正好接地�����。通過(guò)接地節(jié)點(diǎn)“a”���,您可重畫電路并顯示為如圖5所示的更簡(jiǎn)單的版本����。測(cè)試這電路的頻率響應(yīng)并與圖3比較����,以檢測(cè)在新整理出的模型中的任何錯(cuò)誤���。
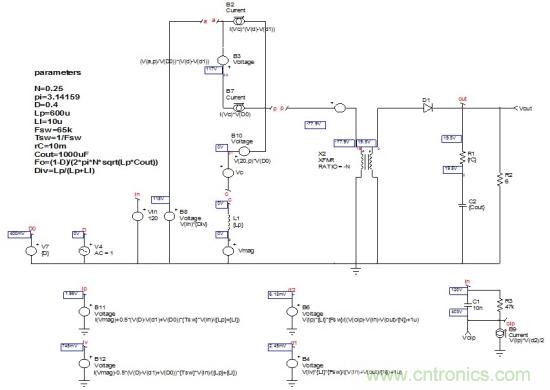
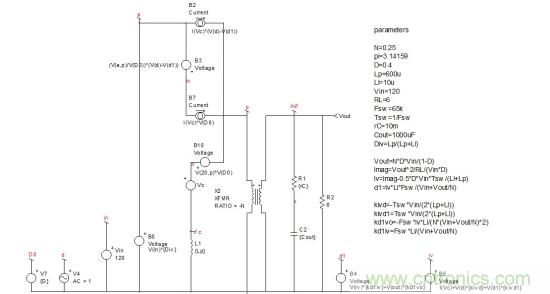
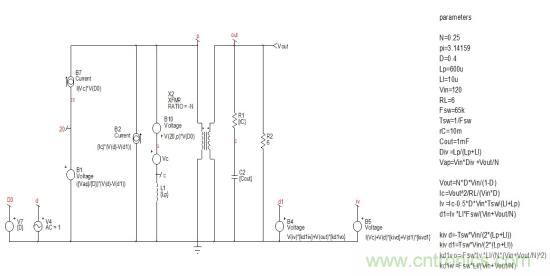
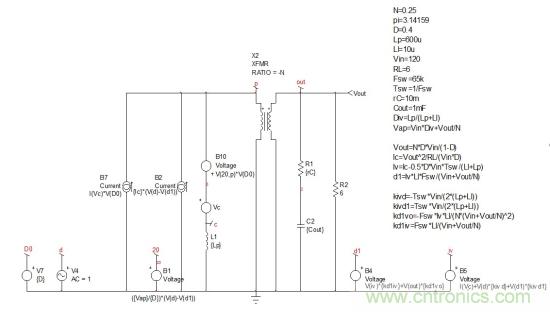
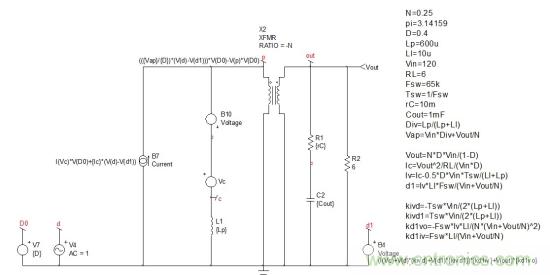
電流源B7與電壓源B1串聯(lián)。為進(jìn)一步簡(jiǎn)化��,B7負(fù)端可參考接地�,而B(niǎo)1的輸出連接到節(jié)點(diǎn)20以獨(dú)立的源轉(zhuǎn)換��。圖6給出了新的電路圖��。節(jié)點(diǎn)20用于源B10(通過(guò)定義更新),兩個(gè)電流源B7/B2可并聯(lián)以形成單個(gè)源�。這是如圖7所示的用于分析的最終電路����。請(qǐng)注意源Iv表達(dá)式已包含在d1源中。基于圖8中的大信號(hào)參考模型繪制此電路的頻率響應(yīng)�����。因?yàn)橄辔缓头迪嗤?����,我們現(xiàn)在可著手這最終的表達(dá)式�。
圖4:更新的電路現(xiàn)在只包括線性源��。
圖5:考慮恒定的輸入電壓,節(jié)電“a”可接地并進(jìn)一步簡(jiǎn)化�����,得出小信號(hào)電路��。
圖6:電流源B7現(xiàn)在接地,而B(niǎo)1在節(jié)點(diǎn)20提供電壓���。
圖7:只要電流源并聯(lián)到B7和節(jié)點(diǎn)20整合到B10��,我們可得出最終的小信號(hào)電路原理圖��。Iv已整合到d1����。
圖8:大信號(hào)模型的頻率響應(yīng)和我們簡(jiǎn)化電路圖7的頻率響應(yīng)相同
生成等式
我們從電感電流等于節(jié)點(diǎn)“c”的電壓除以電感阻抗開(kāi)始��。節(jié)點(diǎn)“c”的電壓由節(jié)點(diǎn)“p”的電壓與電壓源B10串聯(lián)定義。節(jié)點(diǎn)“p”的電壓只是減去通過(guò)變壓器匝數(shù)比N(忽略二極管正向壓降)反射到初級(jí)端的輸出電壓��。我們有
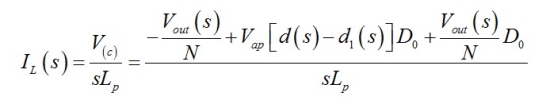
(15)
源d1可改寫,因?yàn)長(zhǎng)p的電流現(xiàn)已被定義(它是圖7 d1源的I(Vc))
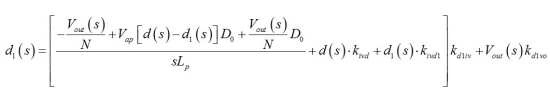
(16)
解得d1(s)為
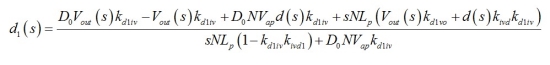
(17)
輸出電流是以變壓器匝數(shù)比N縮放的初級(jí)電流�。它是由源B7減去流經(jīng)電感的電流及由(15)定義的電流:
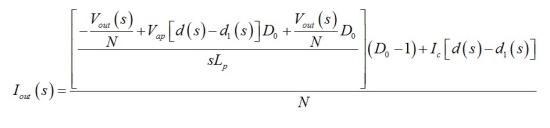
(18)
在此表達(dá)式中�����,Ic是在本系列文章第二部分已確定的直流值
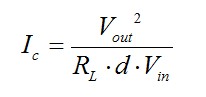
(19)
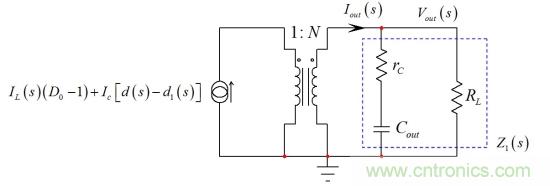
這電流以由如圖9所示的rC,Cout和負(fù)載電阻RL形成的阻抗循環(huán)�����。
圖9:最終描述包括變壓器驅(qū)動(dòng)由輸出電容���、ESR和負(fù)載電阻形成的復(fù)雜的阻抗RL。
這輸出電流也可定義為
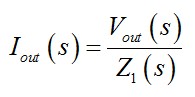
(20)
阻抗可通過(guò)將rC + Cout和RL并聯(lián)或應(yīng)用快速分析電路技術(shù)(FACTS)迅速得出����。重新整理結(jié)果�����,您應(yīng)發(fā)現(xiàn)
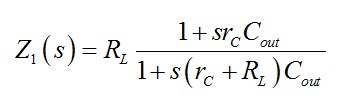
(21)
現(xiàn)在結(jié)合(18)�����、 (20) 和(21)�,我們可寫
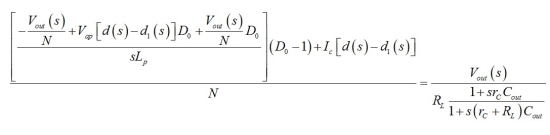
(22)
現(xiàn)在的樂(lè)趣在于求解Vout���,并以二階多項(xiàng)式的形式重新整理傳遞函數(shù)。通過(guò)Mathcad的幫助����,我們得出:
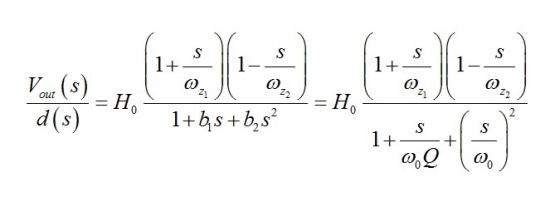
(23)
其中我們已確定以下原系數(shù)
文獻(xiàn)中給出的典型的反激式轉(zhuǎn)換器的傳遞函數(shù)按照(23)的形式并采用下面的定義:
測(cè)試解析表達(dá)式
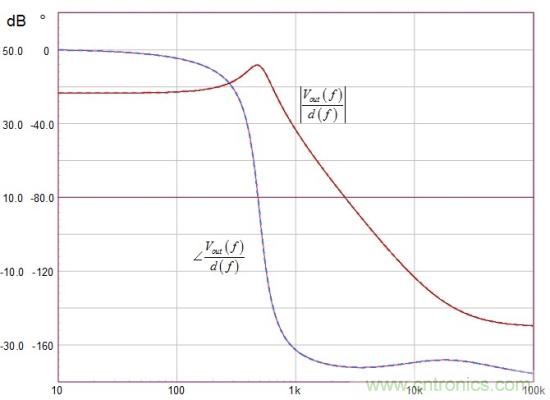
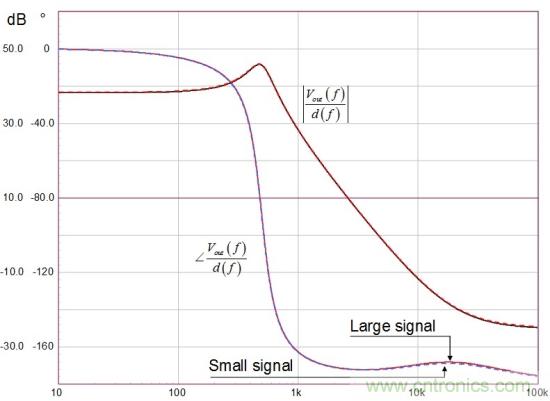
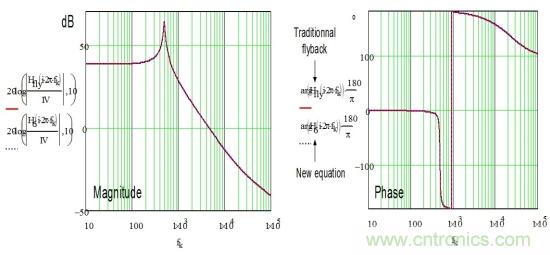
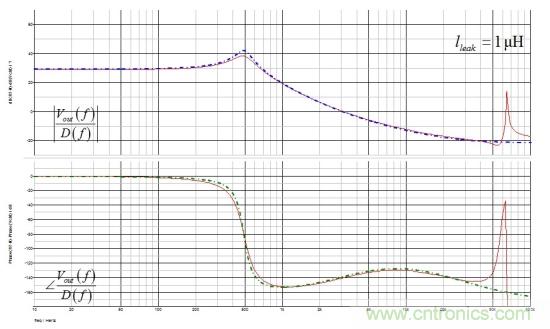
如果我們假設(shè)圖1的運(yùn)行值��,并繪制由(23)給出的響應(yīng),無(wú)論是lleak為0 (rC= 0歐)的復(fù)雜系數(shù)還是簡(jiǎn)化的反激式表達(dá)式����,幅值和相位曲線如圖10所示都完全重疊����。
圖10:當(dāng)漏電感設(shè)為0����,采用復(fù)雜系數(shù)的等式和傳統(tǒng)的反激式表達(dá)式返回相同的頻率響應(yīng)曲線����。
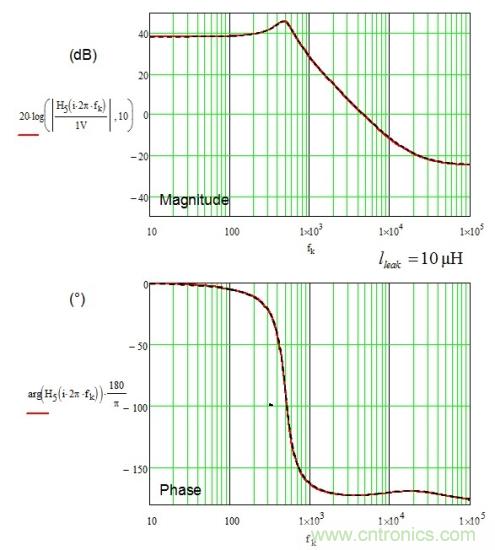
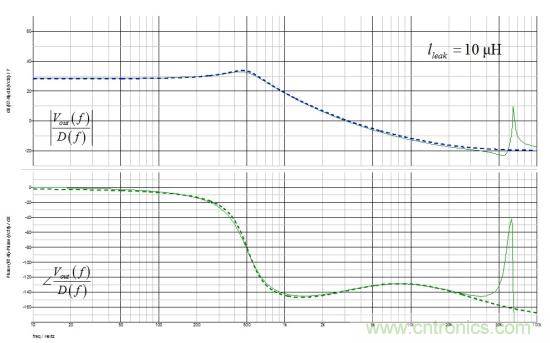
接下來(lái)的測(cè)試包括設(shè)置lleak為10 μH�、疊合由Mathcad和小信號(hào)SPICE仿真得出的曲線�。如圖11所示,曲線的完美重疊證實(shí)了我們對(duì)傳遞函數(shù)考慮漏電感的數(shù)學(xué)推導(dǎo)�����。
圖11:SPICE和Mathcad繪制出完全重疊的曲線���,證實(shí)了我們圖4的關(guān)于傳遞函數(shù)中Vout結(jié)合d的分析推導(dǎo)���。
最后,為將我們的建模方案與另一個(gè)仿真平臺(tái)比較���,我的同事Dr. Capilla采集了在第一部分介紹的以Simplis模板簡(jiǎn)化的逐周期模型����,并運(yùn)行幾個(gè)配置以提取小信號(hào)響應(yīng)����。結(jié)果如圖13所示���,其中我們已粘貼了采用小信號(hào)模型得到的SPICE仿真結(jié)果�����。
圖12:Simplis可提取開(kāi)關(guān)電路的小信號(hào)響應(yīng)
圖13:Simplis的交流響應(yīng)顯示相較SPICE平均模型略有阻尼的電路
對(duì)于1-μH漏電感值��,Simplis顯示出稍低的Q�����,可能是由于仿真電路中一些選定的開(kāi)關(guān)元件固有的損耗��。對(duì)于較高的漏電感值(10和30 μH)�,符合得非常好�����,曲線幾乎重疊�����。
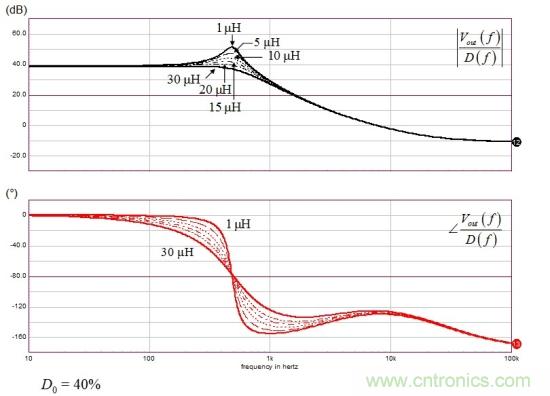
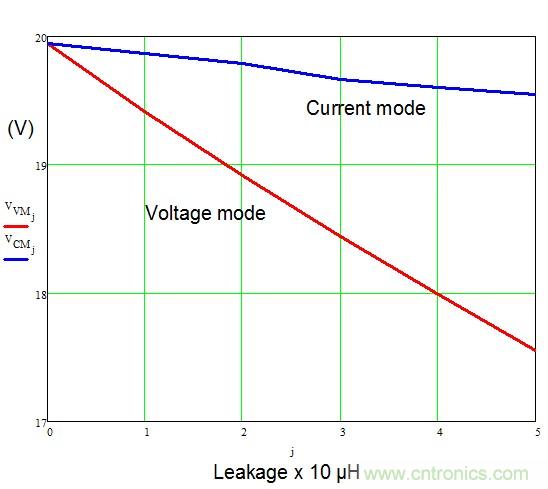
漏電感和品質(zhì)因數(shù)
現(xiàn)在我們的模型是正確的�,我們可交流掃描圖1電路�����,并看漏電感如何影響幅值和相位曲線��。在具低漏電感時(shí)��,Q很明顯,超過(guò)10 dB。當(dāng)漏電感增加����,每切換周期損耗更多能量����,品質(zhì)因數(shù)減弱�����。對(duì)于大電感值30 μH��,系統(tǒng)變得過(guò)阻尼。
圖14:增加漏電感明顯阻尼工作于電壓模式的CCM反激式轉(zhuǎn)換器的響應(yīng)�����。
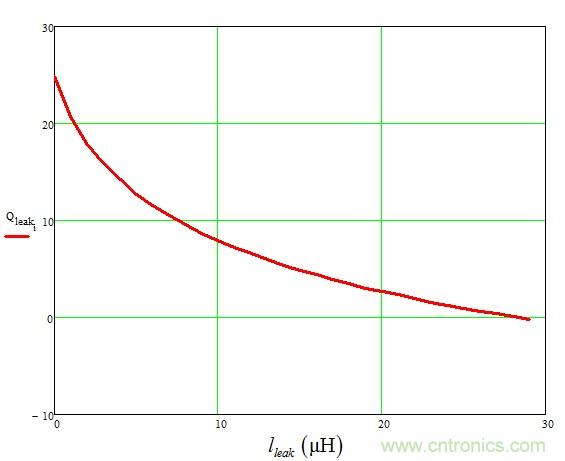
在圖15中���,我們已繪制出Q相對(duì)漏電感的值����,證實(shí)了它對(duì)反激式轉(zhuǎn)換器的阻尼效應(yīng)����。
在電流模式中�,占空比截?cái)嘞?����,因?yàn)楸M管存在漏電感,但峰值電流不受影響���,因?yàn)閠on自然延長(zhǎng)至符合峰值設(shè)定點(diǎn)。如[1]所寫�����,它可標(biāo)明電流模式控制(CCM)中的開(kāi)關(guān)占空比定義為
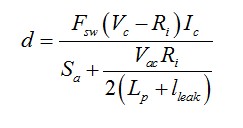
(24)
其中Fsw是開(kāi)關(guān)頻率�����,Vc是控制電壓,Ri是檢測(cè)電阻,Ic是如(19)定義的端點(diǎn)“c”的電流���,Sa是外部補(bǔ)償斜率,Vac是端點(diǎn)“a”和“c”之間的電壓�����。雖然漏電感增加,但有效的占空比(開(kāi)關(guān)占空比由漏電感磁化時(shí)間減少)保持相對(duì)穩(wěn)定���。因此�����,主要是次級(jí)電流的延遲影響了輸出電壓�。但輸出電壓的降低在電流模式控制中低于電壓模式轉(zhuǎn)換器(圖16)��。
圖16:在電流模式中���,峰值電流保持穩(wěn)定��,導(dǎo)通時(shí)間自然延長(zhǎng)以補(bǔ)償漏電感的存在��。因此���,不像電壓模式控制,輸出電壓幾乎不受影響�。
結(jié)論
在這最后一部分����,我們已描述了CCM反激式轉(zhuǎn)換器在電壓模式控制下的控制-輸出的傳遞函數(shù)����。漏電感增加了鉗位源損耗并提供阻尼:傳統(tǒng)的等式?jīng)]有預(yù)測(cè)這一行為��,必須推導(dǎo)新模型���。進(jìn)一步的線性化過(guò)程中�,必須確定性的小信號(hào)傳遞函數(shù)�,表示漏電感對(duì)品質(zhì)因數(shù)的影響。但電流模式控制受漏電感的影響較小�����。參考[2]和[3]指出文獻(xiàn)意識(shí)到漏電感的影響���,但在更新的傳遞函數(shù)表達(dá)式中沒(méi)有規(guī)范地定義這影響��。本文完成了這一工作。
免責(zé)聲明:本文為轉(zhuǎn)載文章��,轉(zhuǎn)載此文目的在于傳遞更多信息���,版權(quán)歸原作者所有��。本文所用視頻、圖片����、文字如涉及作品版權(quán)問(wèn)題���,請(qǐng)聯(lián)系小編進(jìn)行處理���。
推薦閱讀:
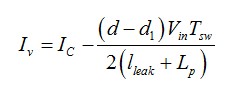 (1)
(1)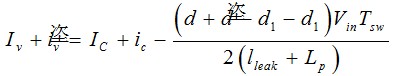 (2)
(2)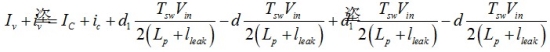 (3)
(3)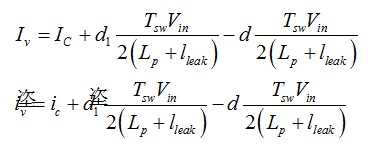 (4)
(4)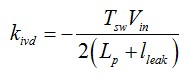 (5)
(5)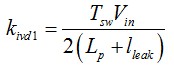 (6)
(6)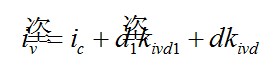 (7)
(7)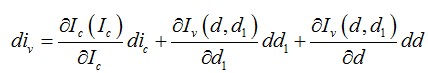 (8)
(8)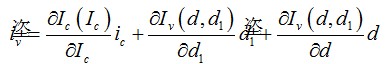 (9)
(9)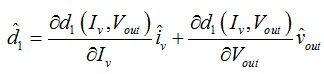 (10)
(10)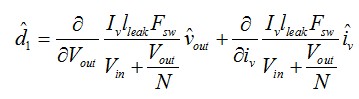 (11)
(11)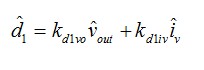 (12)
(12)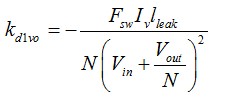 (13)
(13)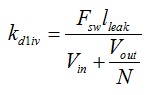 (14)
(14)
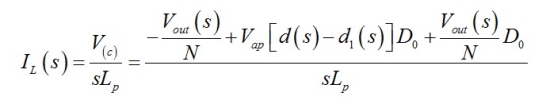 (15)
(15)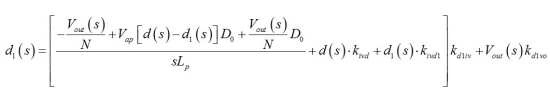 (16)
(16)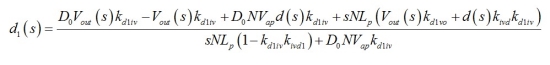 (17)
(17)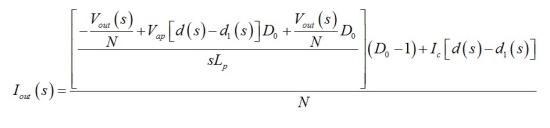 (18)
(18)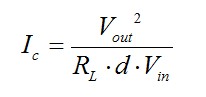 (19)
(19)
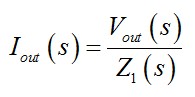 (20)
(20)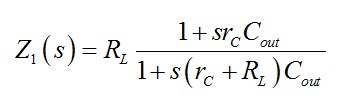 (21)
(21)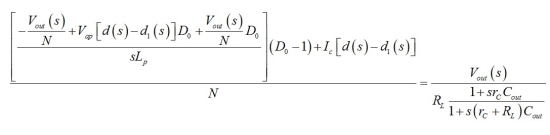 (22)
(22)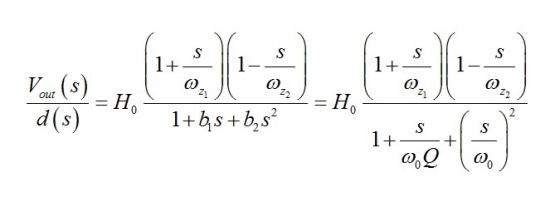 (23)
(23)
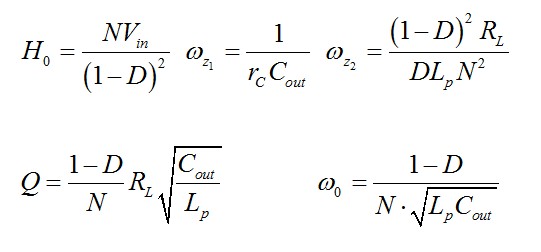

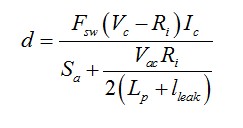 (24)
(24)



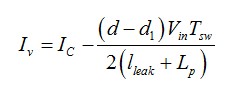 (1)
(1)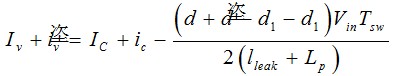 (2)
(2)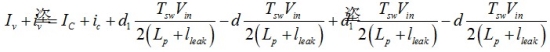 (3)
(3)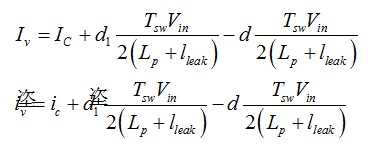 (4)
(4)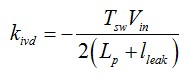 (5)
(5)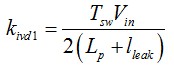 (6)
(6)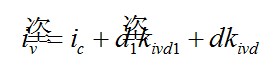 (7)
(7)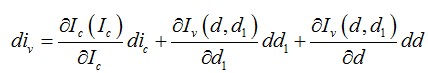 (8)
(8)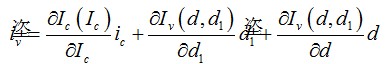 (9)
(9)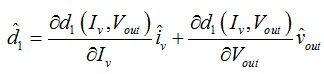 (10)
(10)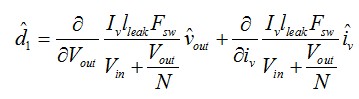 (11)
(11)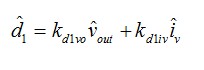 (12)
(12)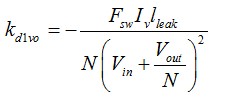 (13)
(13)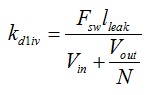 (14)
(14)




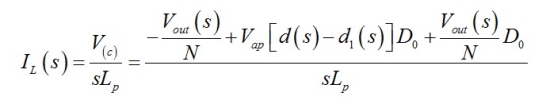 (15)
(15)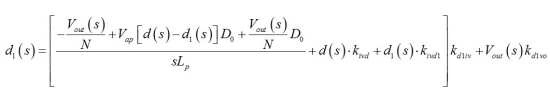 (16)
(16)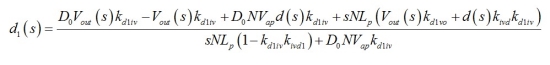 (17)
(17)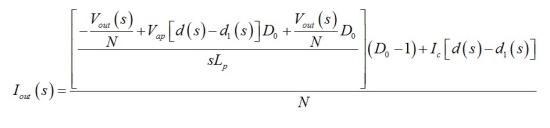 (18)
(18)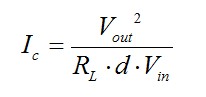 (19)
(19)
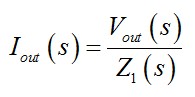 (20)
(20)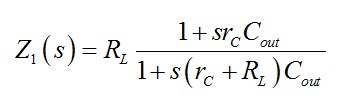 (21)
(21)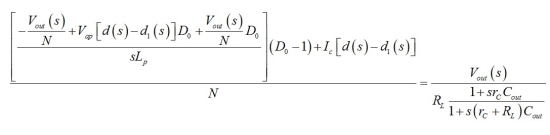 (22)
(22)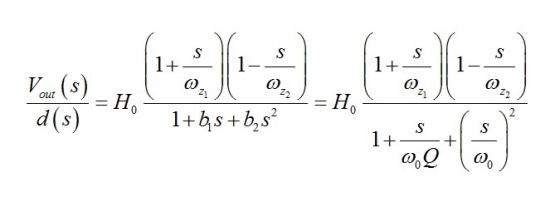 (23)
(23)
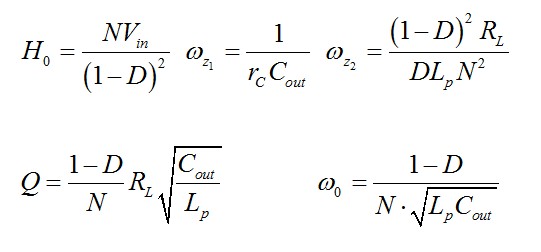








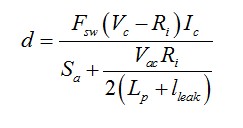 (24)
(24)